Critical Difference Diagram
Critical Difference Diagram
The critical difference (CD) diagrams show the mean ranks of each model under the different masking rates for the test data of the datasets. The lower the rank (further to the left) the better performance of a model under the particular masking rate compared to the others on average. A line in each diagram indicates that there is no significant difference in performance among the models crossed by that particular line in terms of the Friedman test that compares the ranks of multiple classifiers.
Critical Difference (CD) diagrams showing the results of a statistical comparison of the performance of all the heterogeneous ensemble methods, conducted using Friedman and Nemenyi's tests. The groups of methods producing statistically equivalent performance are connected by horizontal lines.
First the Friedman test is performed to reject the null hypothesis, we then proceed with a post-hoc analysis based on the Wilcoxon-Holm method. We can clearly see how on average clf3 and clf5 were the best algorithms over the 15 datasets. A thick horizontal line groups a set of classifiers that are not significantly different.
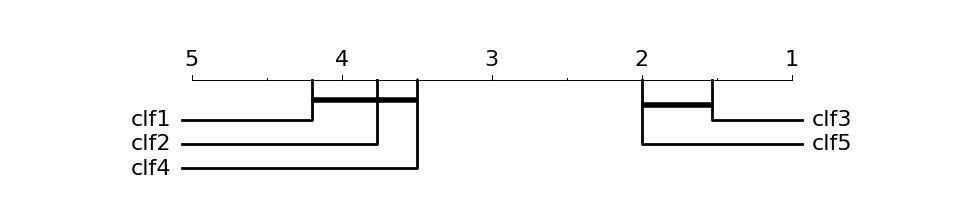
When multiple classifiers are compared, the results of the post-hoc tests can be visually represented with a simple diagram. The top line in the diagram is the axis on which we plot the average ranks of methods. The axis is turned so that the lowest (best) ranks are to the right since we perceive the methods on the right side as better. When comparing all the algorithms against each other, we connect the groups of algorithms that are not significantly different (Figure 1(a)). We also show the critical difference above the graph. If the methods are compared to the control using the Bonferroni-Dunn test we can mark the interval of one CD to the left and right of the average rank of the control algorithm (Figure 1(b)). Any algorithm with the rank outside this area is significantly different from the control. Similar graphs for the other post-hoc tests would need to plot a different adjusted critical interval for each classifier and specify the procedure used for testing and the corresponding order of comparisons, which could easily become confusing.


References
- hfawaz/cd-diagram: Critical difference diagram with Wilcoxon-Holm post-hoc analysis.
- Statistical Comparisons of Classifiers over Multiple Data Sets
